在线资料

中文资料：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes 在线文章：http://www.ai-start.com/ml2014/html/week1.html#header-n257

Linear Regression Model

mind

1. what, fitting a straight line to your data

2. how, build a linear regression model from this dataset

   1. use a dataset on house sizes and prices
   2. plot a graph where the horizontal axis is the size of the house in square feet, and the vertical axis is price of a house
   3. plot the data points
   4. fit a straight line to the data

3. estimate the price(how, predict the price of a house based on the size of the house)

   1. input the size of the house
   2. output price

key word

1. first model
2. That just means fitting a straight line(直线) to your data.
3. let's start with a problem that you can address using linear regression.
4. Say you want to predict the price of a house based on the size of the house.
5. We're going to use a dataset on house sizes and prices from Portland
6. Here we have a graph where the horizontal axis is the size of the house in square feet, and the vertical axis is the price of a house in thousands of dollars.
7. Let's go ahead and plot the data points for various houses in the dataset.
8. Supervised learning model
9. Data has "right answers"
10. Regression model
11. Predicts numbers
12. Regression problem

Part One

Part Two

key word best-fit line

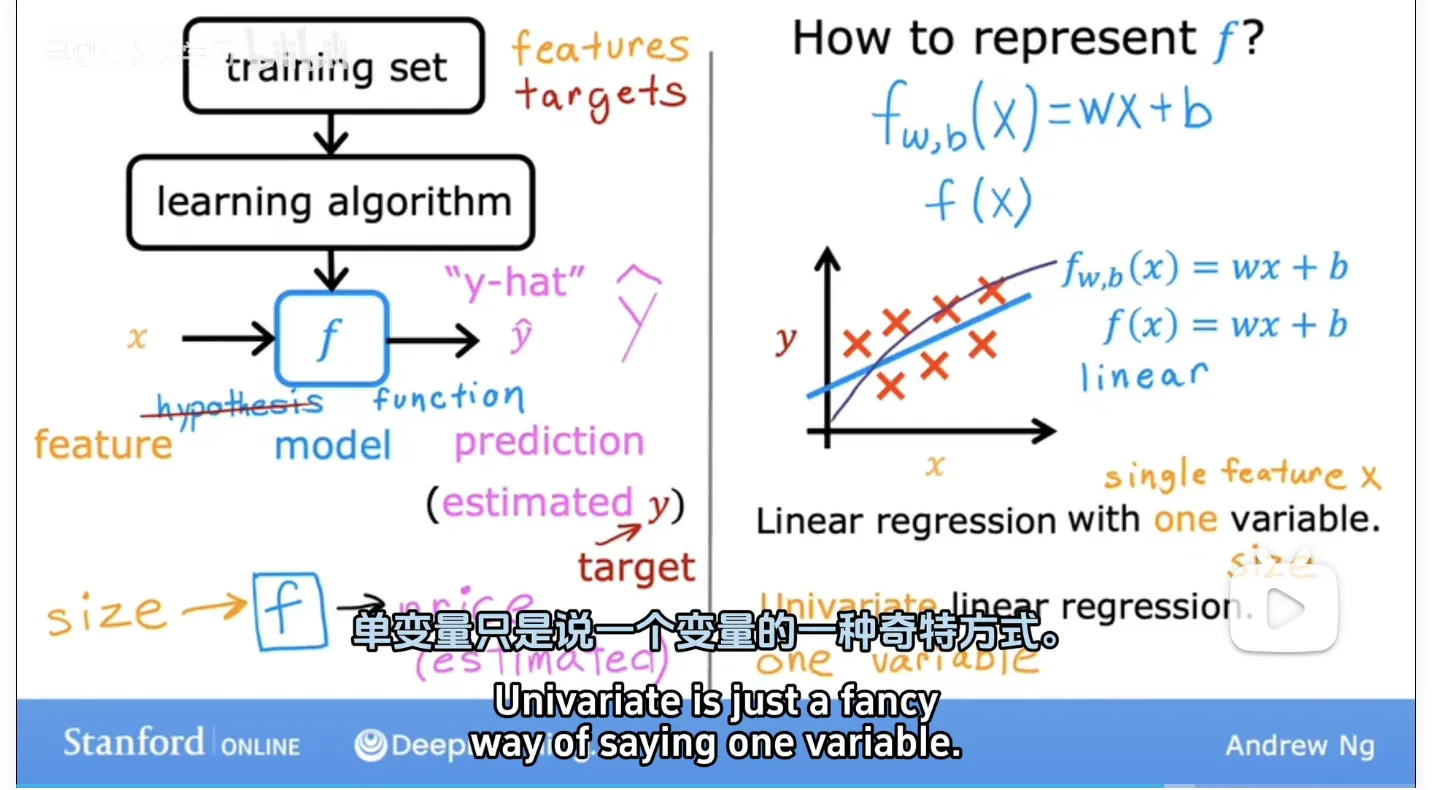
the linear function

why we are choosing a linear function

linear regression

linear regression with one variable = univariate linear rgression

construct a cost function

is the most universal and important ideas in machine learning and is used in both linear regression and in training many of the most advanced AI models in the world

从示例分析流程

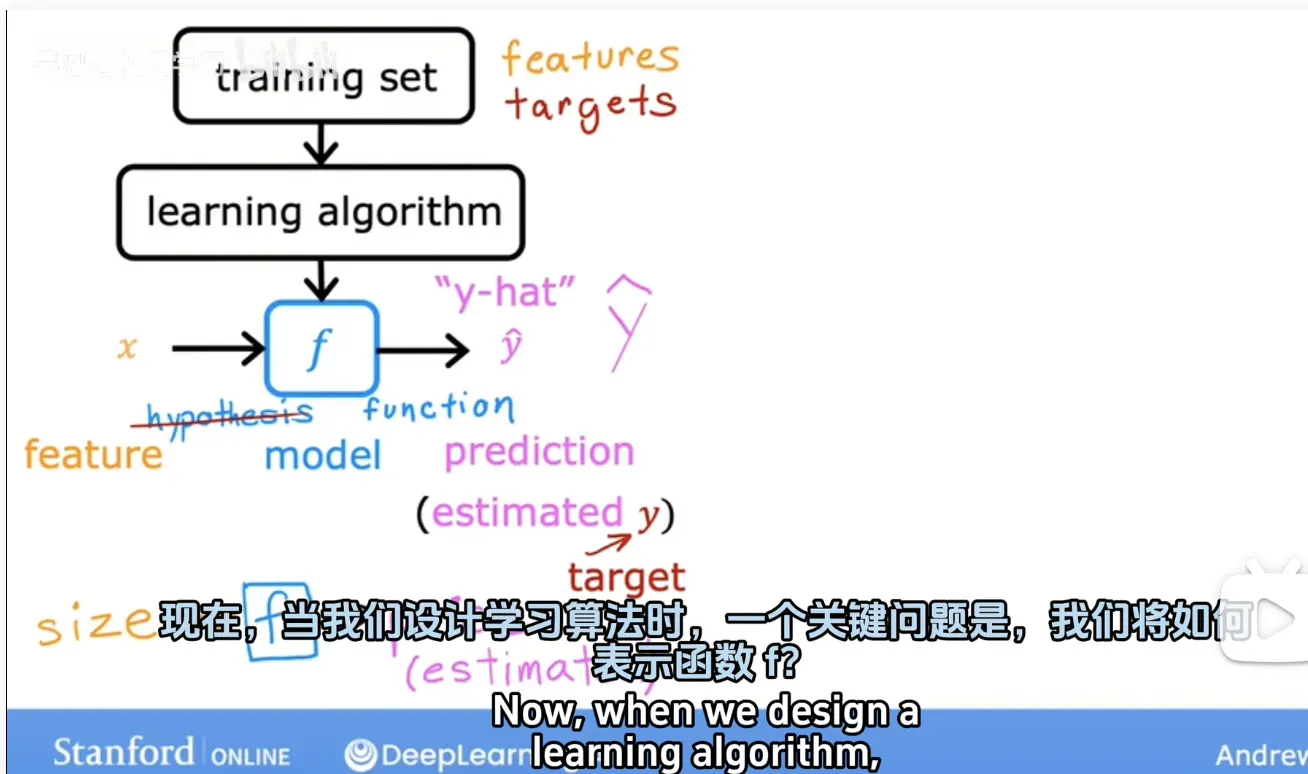
抽象出公式

Cost Function

mind

1. what
2. why need
3. how to formula

key process

**key word **

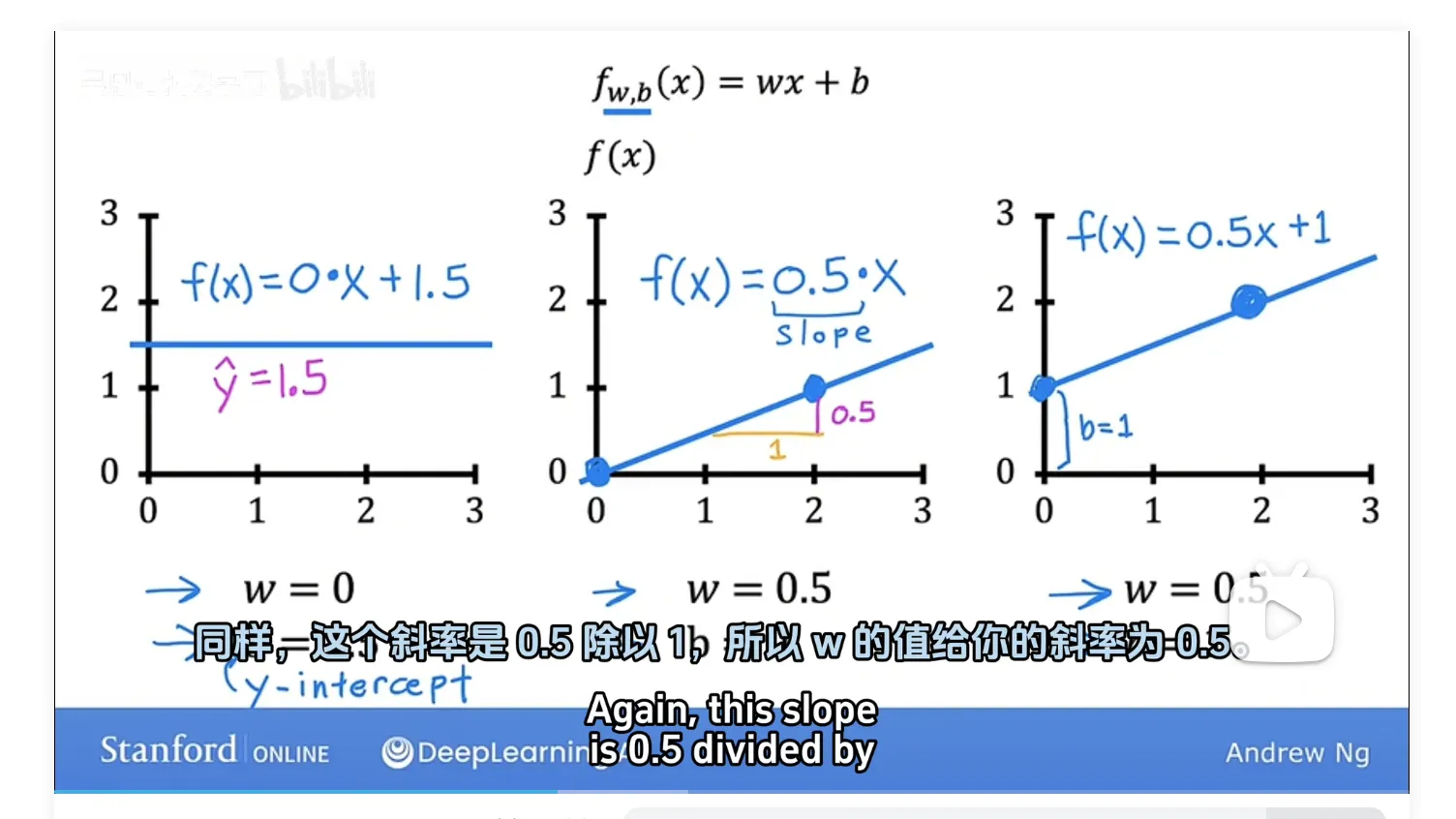
1. parameters、coefficients、weights
2. hellp you build intuition on how w and b the parameters determine f
3. prediction，predictive value
4. slop of the line
5. line intersects
6. superscript ？ 上标
7. y hat i
8. close to the true targe
9. Now the question is how do you find values for w and b so that the predict y hat i is close to the ture target y^i for many or maybe all training examples x^i y^i
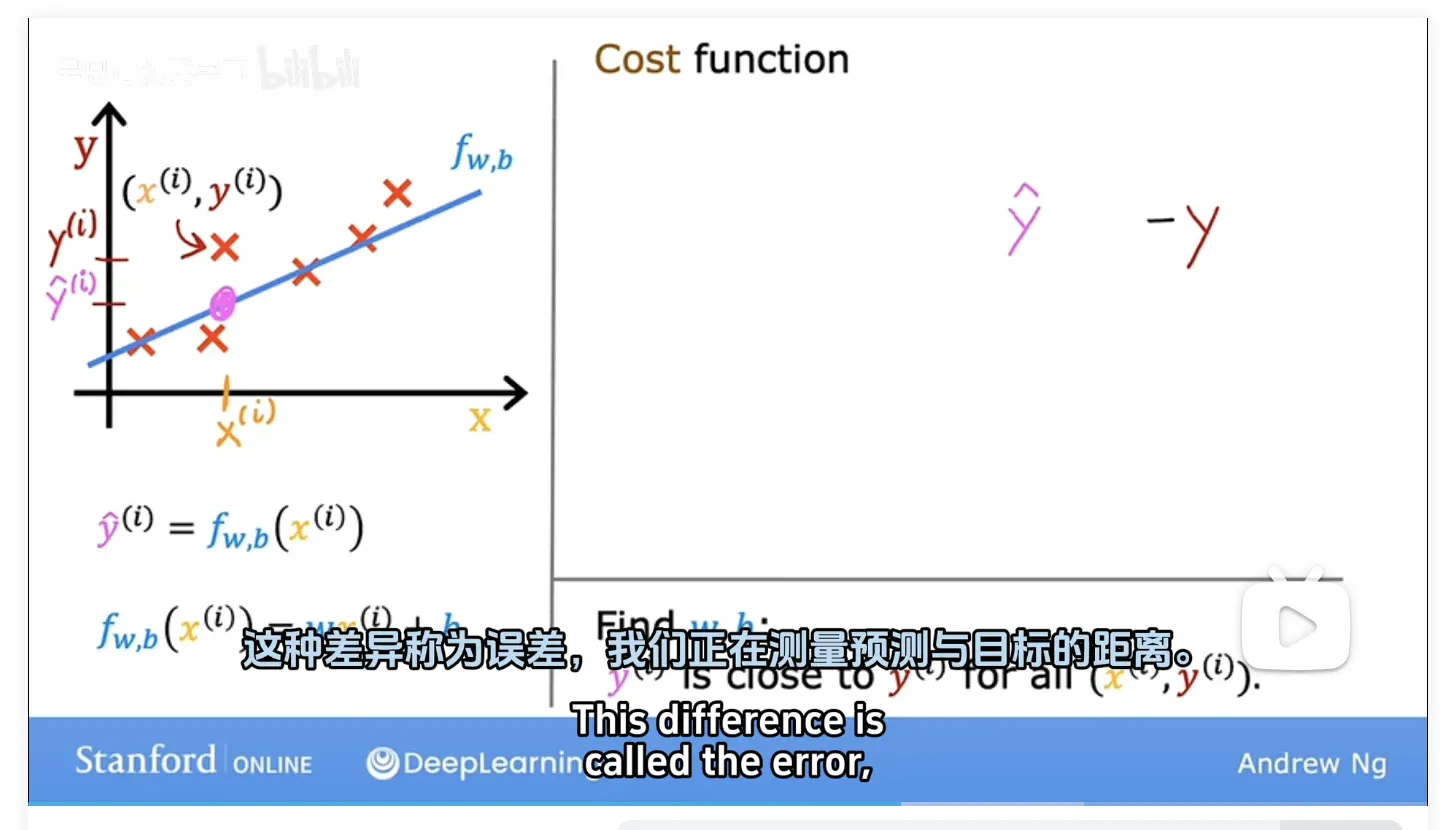
10. how to measure how well a line fits the training data
11. to do that , we're going to construct a cost function
12. The cost function takes the prediction y hat and compares it to the target y by taking y hat minus(减) y.
13. This different called thd error .
14. let's computes the square 平方 of this error.
15. we're going to want to compute this term 项 for different training examples i in the training set .
16. we want to measure the error across the entire 全部 training set.
17. m is the number of training set examples
18. notice that if we have more training examples m is larger and your cost function will calculate a bigger number
19. To build a cost function that doesn't automatically get bigger as the training set size gets larger by convention,we will compute average squared error instead of the total squared error and we do that by dividing by m like this.
20. By convention the cost function that machine learning people use actually divides by 2 times m.
21. The extra division by 2 is just meant to make some of oue later calculations look neater, but the cost function still works whether you include this division by 2 or not.

Cost Function inition

key process

1. define goal

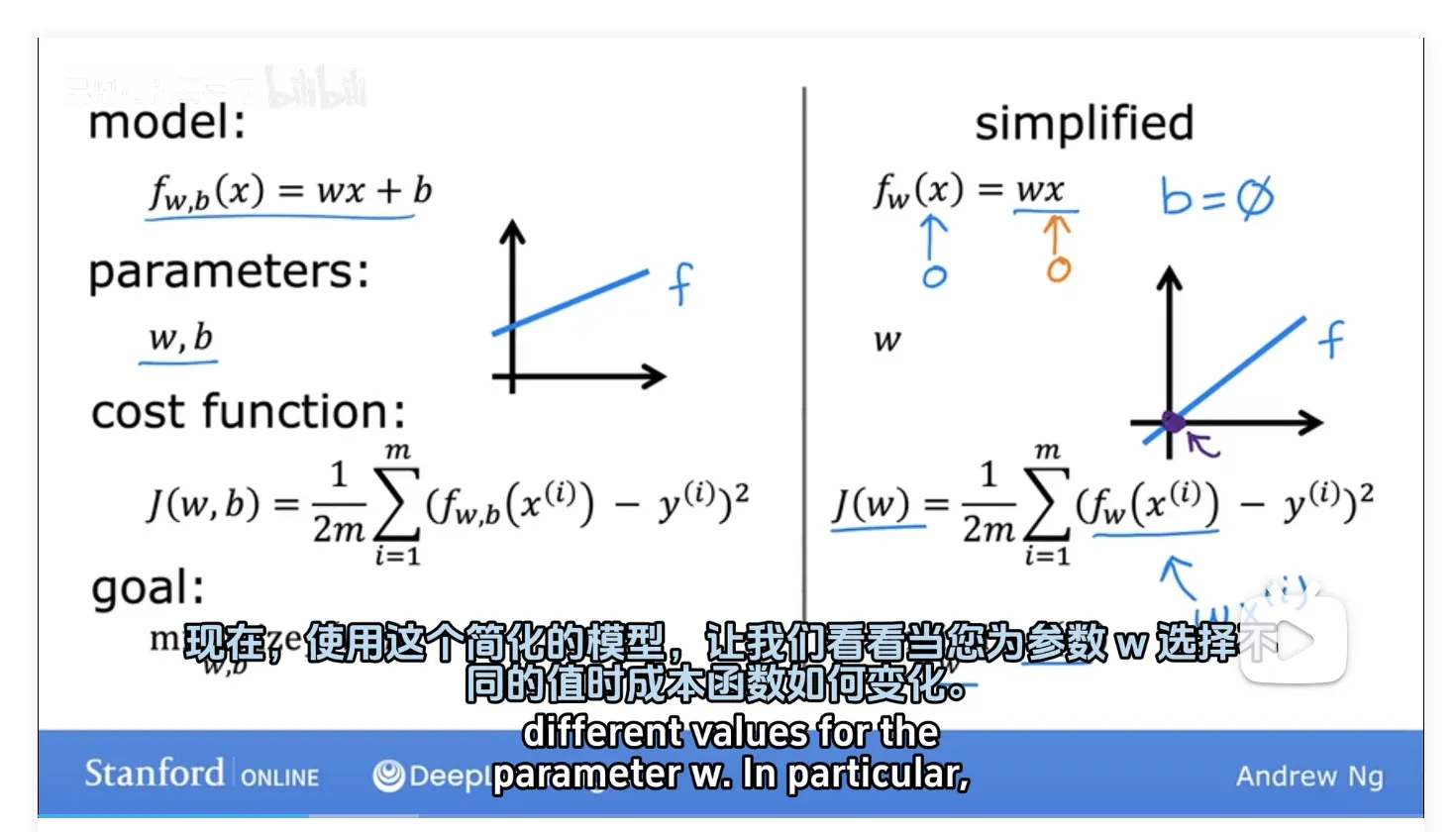
   1. model: you want to fit a straight line to the training data, so you have this model , fw
   2. parameters : the model's parameters are w, and b,
      1. depending on the values chosen for these parameters
      2. ,you get different straight lines like this.
      3. you want to find values for w, and b, so that the straight line fits the training data well
   3. cost function
      1. To measure how well a choice of w,and b fits the training data ,you have cost functiuon J.
      2. What does cost function J dose is, it measure different between the model's predictions and the actual true values for y.
      3. wht you see later, is that linear regression would try to find values for w, and b , then make a J of w be as small as possible.
   4. goal: in math, we want to minimize J 1.

2. simplified

   1. in order for us to better visualize the cost function J.
   2. getting rid of the parameter b
   3. It just goes away from the equation,
   4. so f is now just w times x
   5. the goal become J of w

3. f and j are related

   1. f function , w is constant value , f is only a function of x.

   2. j is only a function of w.

   3. first pick value

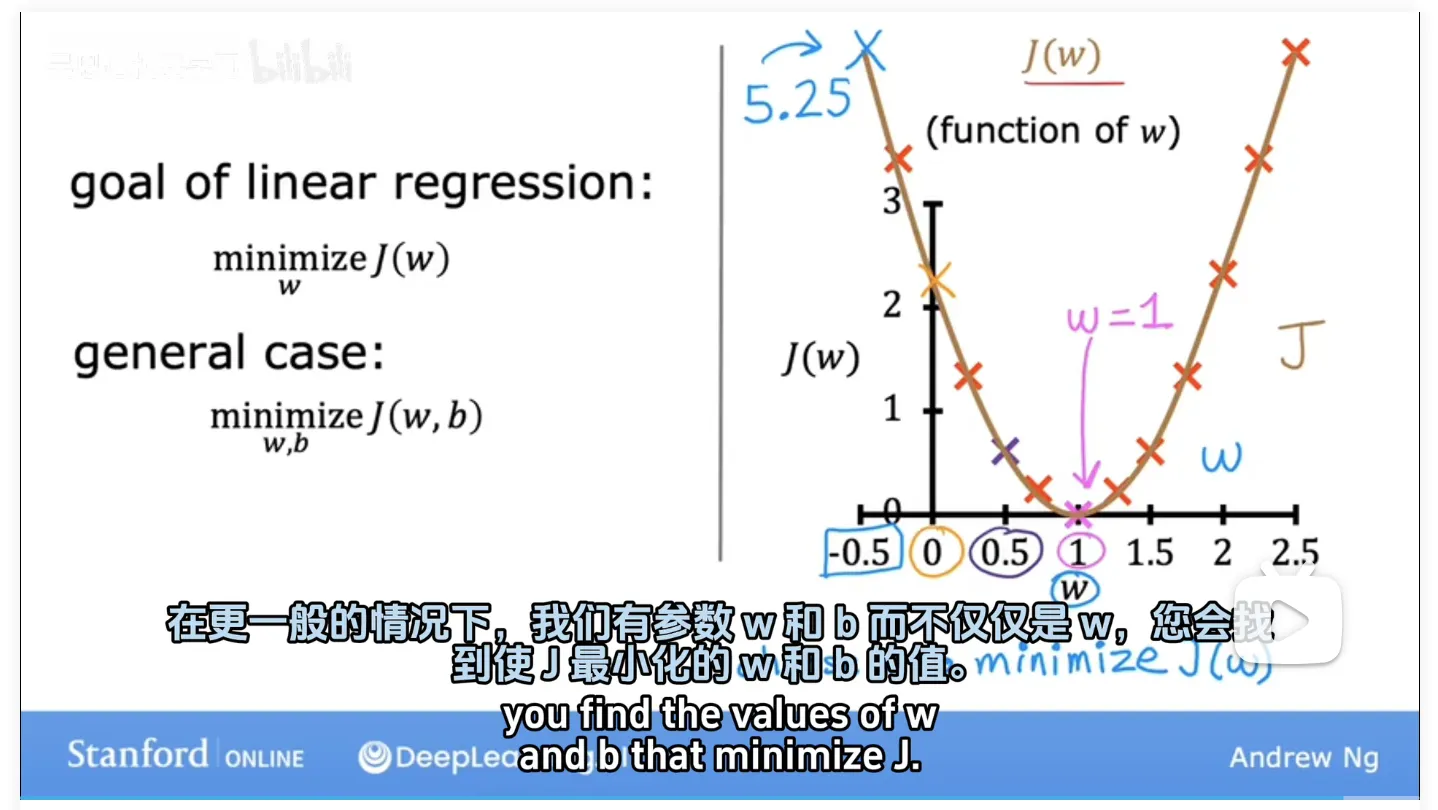
      1. the plots of three points representing，1,1 2,2 3,3
      2. pick a value for w, Say w is 1. 似乎和上一步顺序颠倒，应该先有w，然后在选择f的点位
      3. compute f and j of three point, cost function J is equal to 0 .

   4. let's look at how F and J change for differrent values of w.

   5. second pick value

      1. w is equal to 0.5
      2. comput to y hat of three point
      3. comput to J，we work out the math
      4. The cost J is about 0.58
      5. plot J graph

   6. pick too much values

      1. comput to J，we work out the math
      2. plot J graph

   7. how to choose w ?

      1. Well, as you can imagine, choosing a value of w that casues J of w to be as small as possible seems like good bet.

   8. J is cost function that measures hot big the squared errors are, so choosing w that minimizes these squared errors, makes them as small as possible, will give us a good model.

key word

1. how the cost function can be used to find the best parameters for your model
2. you want to fit a straight line to the training data
3. you have , model , parameters, cost function
4. goal

coursera ppt